Illusions optico-géométriques Ces illusions sont produites par des figures géométriques donnant lieu à des erreurs d'estimation de la dimension, de l'orientation, de la courbure, de la direction ou de la forme de certains de leurs éléments. On considère traditionnellement qu'une illusion géométrique comporte deux éléments : un élément "inducteur" qui provoque une déformation et un élément "test" qui la subit. Perspective Porte Du Savoir

Présentation Les illusions géométriques s'accordent sur trois points fondamentaux. En premier lieu, les illusions sont du domaine perceptif et n'ont rien à voir avec la pensée ou le raisonnement. En effet, vous savez que la plupart des illustrations suivantes sont des illusions géométriques, mais cela ne vous empêche pas de percevoir des déformations. En deuxième lieu, les illusions ne naissent pas dans la rétine ; elles apparaissent presque aussi nettement lorsque l'élément inducteur est placé devant un oeil et l'élément test devant l'autre oeil. Elles prennent donc naissance dans le système visuel au-delà du corps genouillé latéral, là ou convergent pour la première fois les informations en provenance de chaque oeil. En troisième lieu, les illusions ne résultent pas du mouvement des yeux. En effet, elles apparaissent dans toute leur netteté quand la durée d'exposition est trop brève pour que l'œil est le temps de balayer la figure.   Définition La présence de traits suggérant la perspective entraîne des illusions de grandeur. À même grandeur physique, une forme paraissant plus éloignée qu'une autre sera vue plus grande et inversement. On a tenté de généraliser ce principe à plusieurs illusions. Ainsi, l'illusion de Ponzo, qui pourrait être également considérée comme une illusion de mise en relation de grandeur, est fréquemment expliquée par un effet de perspective. De même que l'illusion de Sander qui peut être considérée comme une illusion de perspective, en suggérant que la figure pourrait être vue comme un rectangle présenté en perspective.   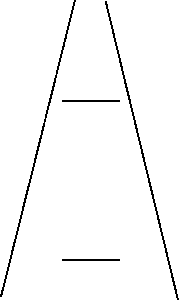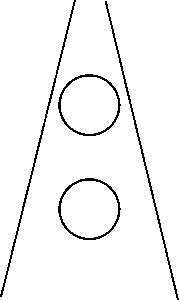Illusion de Ponzo   Illusion de Sander 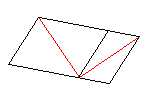La diagonale de droite paraît plus courte que celle de gauche alors qu'elles sont toutes les deux identiques. 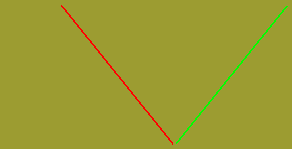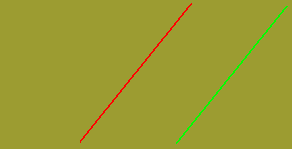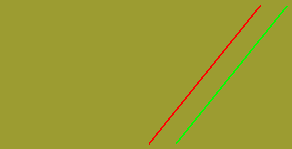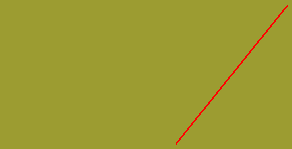Réactualisez la page web (touche "F5" du clavier) pour voir l'exemple en animation !   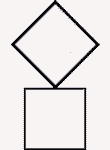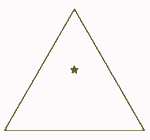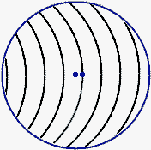Carrés et trapèzes identiques   Point rouge au centre de la figure "Ce site sur les "Enigmes et Illusions", ne serait pas ce qu'il est actuellement sans l'aide de oLIWe, une charmante demoiselle, qui a su donner à ce site des dimensions grandioses." Pepe